System Control Simulation with Python

07 Nov 2018

Reading time ~3 minutes

一、前言

背景

自动控制原理课程以及实验需要用 Matlab 进行系统仿真，需求包括但不限于：

求解拉普拉斯（反）变换。
求解阶跃响应、单位冲激响应。
绘制根轨迹，绘制伯德图等。
绘制以上图像，观察参数影响。

教材：《现代控制系统（十三版）》

虽然 Matlab 功能强大，快捷方便，但是对于我们当下的需求而言，它至少有以下不便：

贵，虽然破解也不能称之为不体面（在中国）。
大，安装和启动一般比较费劲。
窄，虽然可以在各个平台里部署环境，但是从语言的角度，Matlab 不能称得上是一门语言，更难以谈得上封装、移植和维护。

因此，我决定试着用 Python 来实现以上需求，经过一番调研之后发现，不仅实现起来不难，并且配合 Jupyter Notebook（扩展安装 Jupyter Lab）用起来简直不能更爽。这里简单讲讲 Python 实现的系统控制仿真。

课程上大多数人还是用 Matlab，但我希望更多人加入我们 PY 邪教。

环境

Python 3
- control
- SymPy
- matplotlib
Jupyter Notebook
- JupyterLab

二、基于符号库的表达式计算

表达式化简

基于 Symbol 库可以进行表达式化简求值，如教材 CDP4.1 题：

from sympy import Symbol, expand
s = Symbol('s')
Lm = 3.6e-03
Rm = 1.36
Kb = 0.838
Km = 0.8739
Ms = 5.693
Mb = 6.96
Jm = 10.91e-03
r = 31.75e-03
bm = 0.268
Jt = Jm + (Ms + Mb) * r**2
sys = expand((Lm*s + Rm)*(Jt*s + bm) + Kb*Km)
print(sys)

输出为:

8.5194053325e-5*s**2 + 0.033149220145*s + 1.0968082

求值也是可以的，如下（参考运筹学习题 5.1C 2a）：

x = Symbol('x')
f_5_1C_2a = 0.5*(((x + 1)**3 + x**2)**2) - 3

f = expand(f_5_1C_2a)
print(f)
print(f.evalf(subs={x : -0.451}))

输出为：

0.5*x**6 + 4.0*x**5 + 11.0*x**4 + 13.0*x**3 + 8.5*x**2 + 3.0*x - 2.5
-2.93196740658836

以上计算可以解放双手了，更有甚者，再看一个多元函数的例子（参见运筹学习题 5.1B 1f）：

x1, x2, x3 = symbols('x1 x2 x3')
x = np.array([x1, x2, x3])

b = np.array([1, 3, 5])
A = np.array([[-5, -3, -0.5],
              [-3, -2, 0],
              [-0.5, 0, -0.5]])

f = - np.dot(b.T, x) - 0.5*np.dot(np.dot(x, A), x.T)

print(expand(f))

相应输出为：

2.5*x1**2 + 3.0*x1*x2 + 0.5*x1*x3 - x1 + 1.0*x2**2 - 3*x2 + 0.25*x3**2 - 5*x3

偏微分

除了可以进行表达式计算，偏微分运算也是可以的，比如对上一个例子，接着来：

print(diff(f, x1))
print(diff(f, x2))
print(diff(f, x3))

分别输出三个偏微分为：

0*x1 + 3.0*x2 + 0.5*x3 - 1
0*x1 + 2.0*x2 - 3
5*x1 + 0.5*x3 - 5

其中，改成如下这样，结果也是一样的：

a = 'x1'
print(diff(f, a))
print(diff(f, 'x2'))
print(diff(f, "x3"))

三、Documentation & API ！！！

在讲 Python 实现系统与控制仿真之前先多扯几句闲话。

以上操作对大多数人可能有用，也可能有的人不以为意，不过这都不重要，这其实只是一次小小的尝试。

在更多的尝试中，我们会依赖无数轮子，在当“调包侠”的时候，很重要的一点就是查 Documentation 和 API，没有动手实践无法体会到这有多么重要。

建议先查看官方 Documentation、API 和 Demo；出现问题可以查看抛出的异常，浏览 GitHub issues、Stack Overflow 或者 CSDN 等论坛。

其中，十分值得推荐的就是快速查看文档命令：

dir(package)、 help(package)

help to documentation

四、系统与控制仿真

这里用到的最重要的库就是 control，其实查看官方的 Documentation 非常的详尽，琢磨一下问题就不大了，我这里分三个方面给一些简单的例子：

构建系统
系统级联
绘图

构建系统

一般我们都是在 LTI system 的基础上，基于传递函数，构建系统，一般主要来求阶跃响应、单位冲击响应等。构建系统方式有很多，其中最常见的就是基于有理多项式的传递函数的分子和分母构建系统，还是以自控习题 CDP4.1 为例，传递函数为：

$T_s = \frac{K_m}{(L_ms + R_m)(J_ts + b_m) + K_bK_m}$

利用 control.tf 构建系统，不过在此之前可以先对传递函数进行化简：

from sympy import Symbol, expand
s = Symbol('s')
Lm = 3.6e-03
Rm = 1.36
Kb = 0.838
Km = 0.8739
Ms = 5.693
Mb = 6.96
Jm = 10.91e-03
r = 31.75e-03
bm = 0.268
Jt = Jm + (Ms + Mb) * r**2
sys = expand((Lm*s + Rm)*(Jt*s + bm) + Kb*Km)
print(sys)

分母化简得到：

8.5194053325e-5*s**2 + 0.033149220145*s + 1.0968082

再利用 control.tf 分子分母分别按幂次输入系数，建立系统就行了：

import control as ctl
sys = ctl.tf([0.8739], [8.5194053325e-5, 0.033149220145, 1.0968082])

接着就是求阶跃响应和绘图了：

t, y = ctl.step_response(sys)

import matplotlib.pyplot as plt
plt.figure(figsize=(8, 5))
plt.plot(t, y, 'blue', linewidth=0.6)
plt.xlabel('Time/s', fontsize=9)
plt.ylabel('Amplitude', fontsize=9)
plt.title('CDP4.1')

很快就能输出一张阶跃响应图了。

这里需要说明的是，可以不先化简多项式，直接将每个幂次系数表达式输入进去，然后构建系统。这样完全没问题，但是我分开来做主要是有三个原因：

Jupyter Notebook 是一个交互式的编辑器，如果成功部署过并用熟之后就能深切体会到交互式的好处了。加之 Python 比较灵活，我可以插入很多代码块，每块之间有联系，数据可以调用，但是又可以稍微独立一些而减少一些耦合。比如，上一块我就用来化简，下一块再直接用得到的数据，这样构建系统那里会更加纯粹一些，用起来也更加灵活。
我懒得算每个幂次的系数表达式。
看着舒服。

在我的 Jupyter Lab 中效果如下：

result

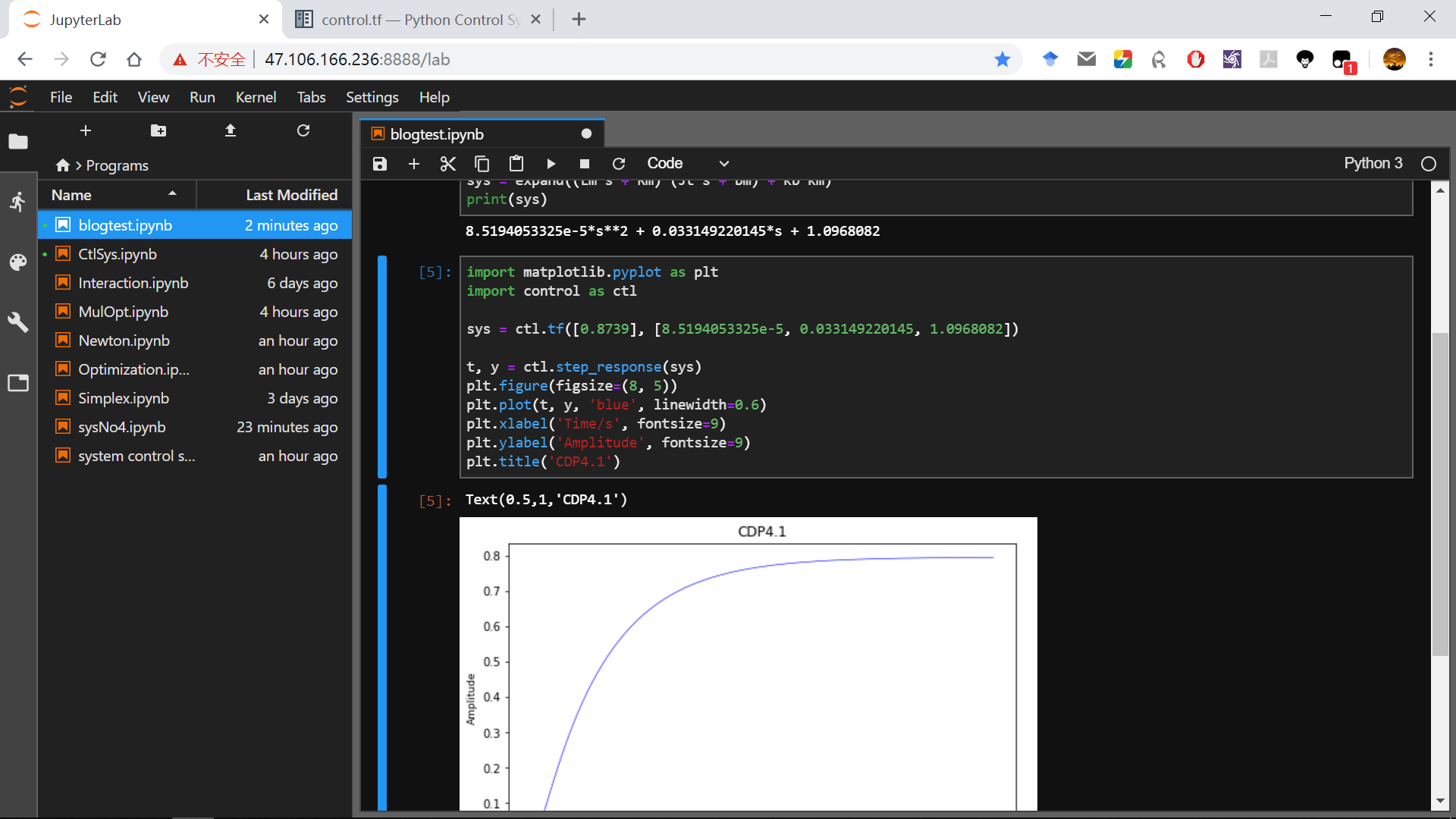
系统级联

除了求系统响应，接下来用的很多的就是系统的反馈求解，当然我们可以手动先求解出系统级联之后的传递函数，然后再进行同样的求解，但是这样一般比较麻烦，其实库里面有 system-interconnections 相关的函数可以调用，最常用的就是 feedback，同样习题 CDP4.1 的反馈为例，值得注意的是，虽然是单位负反馈，但是反馈函数的类型的转化一下，具体要求见官方文档，这里给出一个例子。

k = 10
t, y = ctl.step_response(ctl.feedback(k*sys, ctl.tf([1], [1])))

之后绘制图像就是一样的了，如果要多个曲线绘制在一个图里，则需要去研究一下 matplotlib.pyplot 了。

五、交互部件

既然都用上 Python 和 Jupyter Notebook 了，怎么会轻易就满足了，我之前在服务器的 Jupyter 上扩展了 ipywidgets，可以调用函数进行一些小交互。

起初配置 ipywidgets 只是看着有意思，但是突然想到可以跟系统与控制仿真结合起来，利用交互小部件获取参数，实现动态调参，试了一下：

from IPython.display import display
import ipywidgets as widgets
import matplotlib.pyplot as plt
from control import *

k = widgets.IntSlider(min=1, max=100,  description='k:')

def sysPlot(k):
    sys = tf([0.8739], [8.5194053325e-5, 0.033149220145, 1.0968082])  
    t, y = step_response(feedback(k*sys, tf([1], [1])))  
    plt.figure(figsize=(8, 5))
    plt.plot(t,y,'blue',linewidth=0.6)
    plt.xlabel('Time/s',fontsize=9)
    plt.ylabel('Amplitude',fontsize=9)

out = widgets.interactive_output(sysPlot, {'k': k})
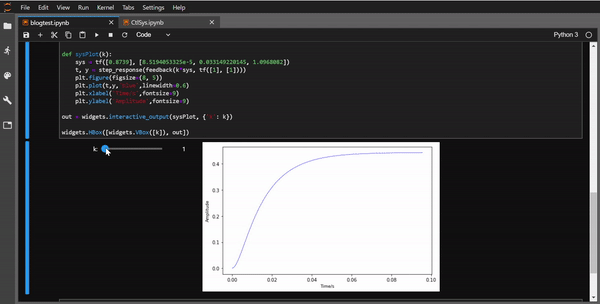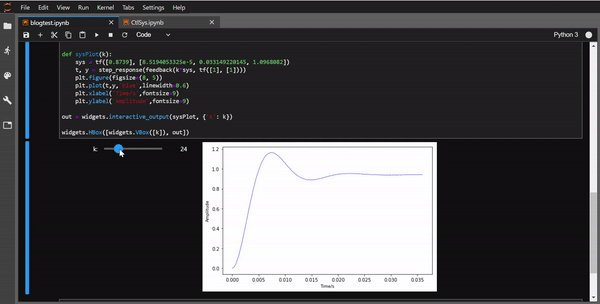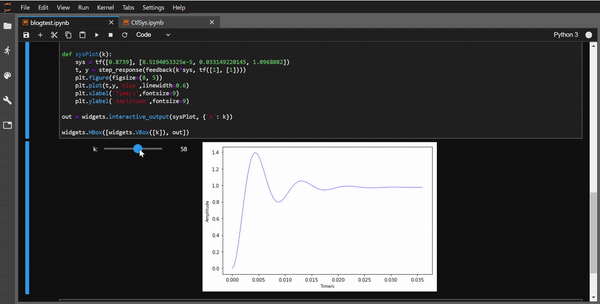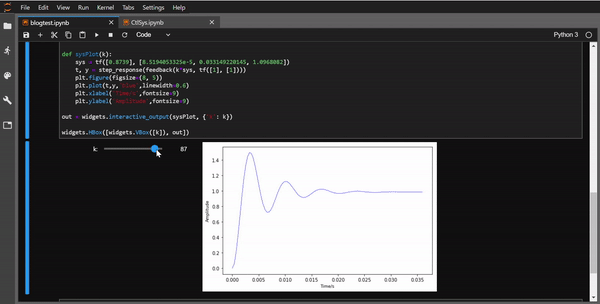
widgets.HBox([widgets.VBox([k]), out])

效果如动图所示：

interaction system

六、结语

以上有很多语法与 Matlab 差不多，所以如果你对用 Python 还是不以为意，那就算了。
建议部署并使用 Jupyter Notebook，尤其是部署到服务器上。简单来说 Jupyter 是一个支持很多种语言的交互式代码编辑器，其中插入的 cells 还可以选择是代码块或者 Markdown，所以我的实验报告基本也在上面写了。打开浏览器输入 ip:port 就行了，敲代码，或者 Markdown（嵌 LaTeX 和 HTML）生成 PDF，由于在服务器上不用本机跑，所以也不卡，用过就知道爽。
关于服务器部署 Jupyter、Shiny、MediaWiki、SS，或者基于 GitHub Pages 用 jekyll 简单地搭建这样一个小博客（~~别人的轮子~~）, 有空就写写（~~当然一般是没空的~~），这篇博客就作为一篇尝试。